Kontinuierliche Wiederanlage

Bei kontinuierlicher Wiederanlage werden Zinsen augenblicklich gut geschrieben und erneut verzinst. In der Zinseszins Formel geht die Wiederanlagefrequenz daher gegen unendlich.

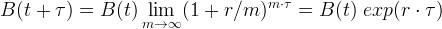m ⋅τ B (t + τ ) = B (t)mlim→ ∞ (1 + r ∕m ) = B (t) exp (r ⋅ τ)

(6)

In Gleichung (6) bezeichnet τ den Anlagezeitraum in Jahresbruchteilen, exp ist die Exponentialfunktion zur Basis e ≈ 2.71828 und r die kontinuierliche Rendite. Somit beschreibt Gleichung (6) ein exponentielles Wachstum des Anlagebetrags B. Nun kann Tabelle 1 vervollständigt werden: 1000 Euro wachsen bei 4% kontinuierlicher Rendite nach 10 Jahren auf 1491.82 Euro an. Verzinsung mit kontinuierlicher Wiederanlage kommt nicht im Privatkundengeschäft vor. Sie kann als finanzmathematisches Konstrukt verstanden werden, welches bei der Entwicklung von Preismodellen für komplexe Finanzinstrumente hilfreich ist. Eine kurze Herleitung kann den Nutzen verdeutlichen. In den vorangegangenen Kapiteln wurden Zinserträge für definierte Anlagezeiträume gutgeschrieben und erneut angelegt. Man spricht diesbezüglich auch von Verzinsung mit diskreter Wiederanlage, deren zeitlicher Verlauf mittels einer Rekursionsformel beschrieben werden kann.

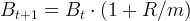B = B ⋅ (1 + R ∕m ) t+1 t

(7)

In Gleichung (9) ändert sich der Anlagebetrag B in diskreten Zeitschritten Δt = 1 ∕ m. Bei wiederholter Anwendung der Rekursionsformel entspricht der zeitliche Verlauf des Anlagebetrags dem der Zinseszins-Formel (4). Durch Subtraktion von B_t auf beiden Seiten kann die Rekursionsformel in eine Differenzengleichung umgestellt werden.

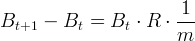1 Bt+1 - Bt = Bt ⋅ R ⋅ --- m

(8)

Wegen Δt = 1 ∕ m folgt

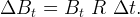ΔBt = Bt R Δt.

(9)

Bei kontinuierlicher Wiederanlage gehen die Zeitschritte Δt gegen Null und aus der Differenzengleichung (9) wird eine Differenzialgleichung (10) mit der kontinuierlichen Rendite r(t).

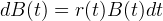dB (t ) = r(t)B (t)dt

(10)

Die Entwicklung von Preismodellen wird erleichtert, weil die Funktion B(t) nun kontinuierlich und differenzierbar ist, solange dies auch für die Funktion r(t) zutrifft. Mit diskreten Zeitschritten wie in Gleichung (9) ist der Betrag B(t) hingegen eine Treppenfunktion, die zum Ende des jeweiligen Anlagezeitraums Δt auf den nächst höheren Wert springt. Bei kontinuierlicher Wiederanlage kann man eine Funktion für B(t) bestimmen, indem man die Differenzialgleichung (10) durch Integration löst. Hierzu dividiert man zuerst beide Seiten durch B(t).

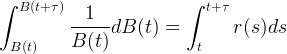∫ B (t+ τ) ∫ t+ τ --1--- dB (t) = r (s)ds B(t) B (t) t

(11)

Die Stammfunktion zur linken Seite der Gleichung (11) ist der natürliche Logarithmus, so dass sich folgende Lösung ergibt:

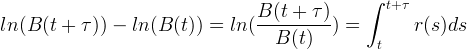∫ B (t + τ) t+τ ln (B (t + τ )) - ln (B (t)) = ln (----------) = r(s)ds B (t) t

(12)

Wenn wir auf beide Seiten der Gleichung (12) die Exponentialfunktion anwenden, ist das Ergebnis die allgemeine Formel für Verzinsung mit kontinuierlicher Wiederanlage.

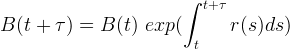∫ t+ τ B (t + τ) = B (t) exp ( r(s)ds ) t

(13)

Für eine zeitinvariante kontinuierliche Rendite r entspricht diese Formel Gleichung (6) vom Anfang dieses Kapitels.

Literatur

Bodie, Zvi and Robert C. Merton, Finance, first edition ed., Pearson Education, July 2000.

Brigo, Damiano and Fabio Mercurio, Interest Rate Models – Theory and Practice, second edition ed., Springer, 2007.

Estrada, Javier, Finance in a Nutshell, first edition ed., Financial Times/Prentice Hall, August 2005.

<Zurück

Literatur

Cookie-Einstellungen